信息过量

庫得克国际 Dr Juergen Ude  王文艳译 

分析是指将数据转化成信息，从而帮助人们做决策。但是到底需要多少信息呢？这篇文章将谈一谈信息过量的问题。如果往桶里倒水，那么总有一个时刻，水满了会溢出来。如果用这桶水来灭火，则多余的水并没有起到作用，完全是浪费了。信息过量是针对某个目标，提供过多且无用的信息。我们将用一个例子来进行阐述。

例如在质量保证中普遍应用到的过程性能分析，这种分析也能应用到其他许多领域，例如，血压监控。在很多过程性能报告中会看到以下输出结果。

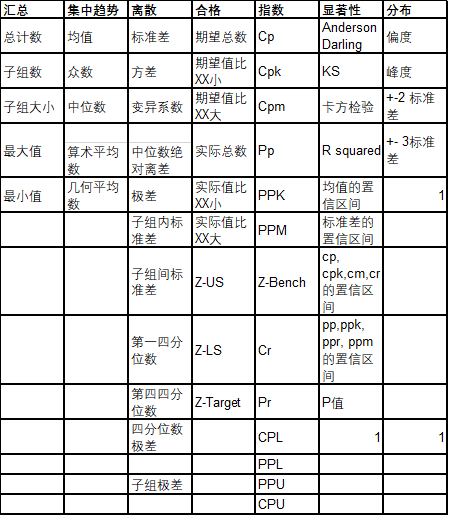
表I 

一些分析报告甚至包含更多的统计量。这些信息可能对组织中的某个群体很有吸引力，他们喜欢尽可能多的信息，但真正的专家会质疑需要这么多信息的必要性。提供过多信息的风险在于，用户会不知所措，困惑不已，且会错过性能分析结果中的重要部分。

信息过量可以定义为在执行某项任务时，提供不必要的信息。以上列出的统计量可能确实很多，但它们真的有必要吗？它们的目的是什么？目的和目标是一致的吗？应该报道的最少信息量是什么？最多的信息量又是什么？遗憾的是，并没有公式可以计算出优平衡量。每种情形要结合其自身特点具体分析，要考虑到方方面面。接下来我们将结合上述例子，对判断哪些信息有用，哪些信息没用的过程进行讨论。 

在统计学研究中，有个术语叫“充分性”。如果所给的样本中得出的其他统计量对于统计值提供不了更多信息，则该统计量是充分的。例如，样本均值是一个充分统计量。因为没有其他统计量可以提供关于平均数的更多信息了。 

这个原理可以部分应用于判断某个信息是否充分。任何多余的信息都是信息过量。在这种情况下，我们谈论的不是统计量，而是满足某个目标的信息，包括图（目标是什么的确使情况更复杂，因为目标可能有很多，这一点也会越来越明显）。 

乍一看，过程性能研究的目的是从生产不合格品的角度了解当前过程运作的有多好。满足这个目标，需要的最小信息量是多少？ 

直方图，如下图所示，提供过程性能方面的信息。一眼就可以判断过程性能的好坏。它是充分还是不充分呢？

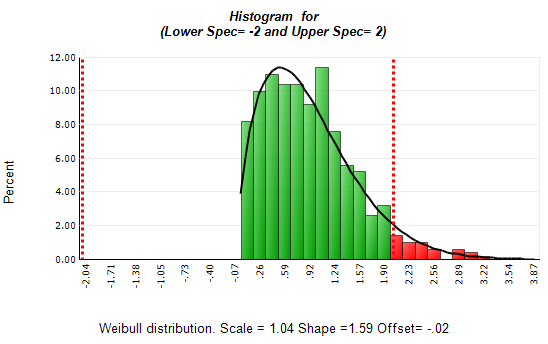
图1：直方图举例

如果唯一的目的是参照规格限判断过程表现得怎么样，且样本数量很大，那么显示规格限的直方图是充分的。不需要其他统计信息，任何多余的信息都会造成信息过量。

但是，如果样本数量少，则信息不充分。原因是抽样误差。抽样误差可能会使不合格方面的真实性能估计值放大或缩小。因此，我们需要缺陷比例的置信区间，以便在可靠性方面对结果进行分析。

如果样本量小，那么我们甚至不需要直方图。置信区间就够了。没有其他信息或统计量能够更好的说明这个问题。

如果目标不仅仅是从生产不合格品的角度了解当前过程运作的有多好，还包括要了解为什么会这样，则也需要直方图。直方图会显示不合格品是由中心偏离或过程能力导致。它也能判断零不合格品是否由操作员篡改造成的。是指为了避免调整过程，操作员伪造合格结果。

因此，要从生产不合格品的角度了解当前过程运作的有多好，且要了解为什么会这样，过程直方图和不合格品的置信区间是充分的信息。任何其他信息都会造成信息过量。

如果目标是还要对不合格品数量进行估计。例如，要判断期望保修成本，则尽管置信区间很重要，但此处就不合适了。出于会计原因，需要单点样本估计值。但基于实际的不合格品的估值是不充分的。如果估值是0，且样本大小小，则这个结果可能具有误导性。这些额外信息可从理论分布获得，通过比较期望和和理论分布得到一个均值。

理论估计也可能不充分。结果取决于受样本大小影响的拟合分布。需要实际估值和理论估值获取更全面的估值。

因此，如果目标是通过不合格品的估计来判断过程性能，如果样本量小，则直方图，观测得到的不合格品置信区间以及理论和实际不合格品的估计都需要。不需要的是Zu和ZL值，他们是通过假设的理论分布计算期望不合格品数时使用的中间值。同样的，PPL和PPU是用于获取PPK值的中间信息。中间结果并不起什么作用，只是增加了过量的信息。

过程性能分析很少是“快照”式分析。过程性能分析在实际情况中，频繁的进行过程性能分析用于检测过程性能的变化。快照分析强有力的直方图，在比较随时间或产品间变化时，并不适用。因此我们需要量化性能。不合格百分比倒是可以用于这两种比较，但是，过程多紧凑，集中和瞄准目标，它就没法提供信息了。Pp, pr和ppk过程性能指数更合适，但不充分。可计算时，会要求置信区间。而在非正态分布时，这又不太可能。

除此之外，如果要做到充分，分布分析的结果也是需要的，因为这些指数取决于拟合的分布。要验证这些性能指数，必须有强有力的证明表明拟合正确的曲线。拟合曲线的直方图看上去倒是可以提供充足的信息，但实际上它并不能。看看下面图片中的曲线就明白了！

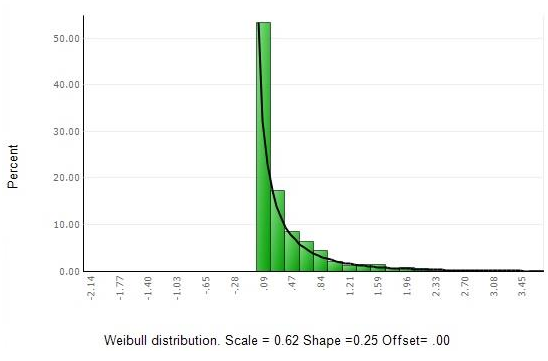
图2：拟合的威尔布尔曲线和强倾斜的数据

这个拟合看上去不错，但真是这样吗？和下面直方图中的拟合比较一下看看！ 

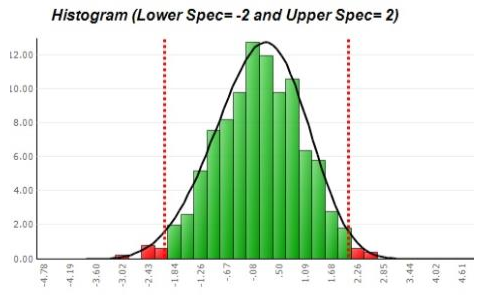
图3：拟合的正态曲线和对称分布

拟合的更好一些了吗？我们需要结合其他信息来回答这个问题。

概率图提供这样的信息。比较下面的两个概率图。第一个对应图2，第二个对应图3。

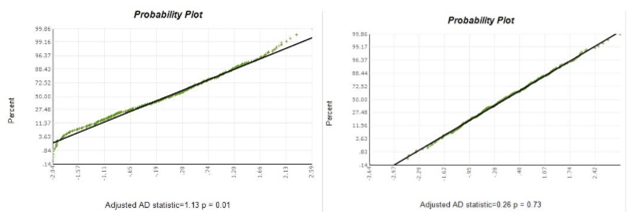
图4：比较两个概率图

我们可以看出，第二个拟合的更好。Anderson Darling统计的p值也能证实这个结果。极限值处不好的拟合表明，极值处的不合格品比例的理论估值必须谨慎处理。

我们可以得出结论，要实现多目标的过程性能分析，所需要的最少的充分信息有：

● 直方图

● 概率图

● 拟合曲线的显著性检验

● 期望的不合格品数和理论的不合格品数

● pp（和相关的pr），ppk指数

● 这些指数的置信区间

这满足以下目的

●  获得当前过程性能的快照

● 获得不合格品，集中，比较，监控和报告的展布度的可量化信息

● 分析的置信

如果瞄准过程也重要的话，可以在上述目的中加上目标偏差。Ppm是另外一个测量目标的统计量，但是理解起来比较困难，也只能用于正态分布的数据。它不是稳健的信息。出于这个原因，BISNET Analyst使用目标偏差，相关的规格极差使用目标偏差百分比。

大多数的输出结果提供了额外的汇总信息，包括平均值，标准差，最.大值，最小值，极差和计数。尽管有些信息在计算时可能会用到，但要满足目标，报告时却不需要。

上表中其余的信息也就是：

众数，中位数，几何平均数，下四分位数，上四分位数极差，平均偏差，子组大小，子组数量，子组内标准差，子组间标准差，ZI，Zu，CpL，CpU，cp，cpk，cpm，其他的统计检验，例如，卡方检验，KS检验，偏斜度，峰度，±2σ，±3σ，在满足目的时，并不需要这些信息。因此这些造成信息过量，让人困惑，且让人看不清最重要的信息是什么。它们可用于分析其他目的。

BISNET Analyst不属于认为信息越多越好的流派。它将以最小量的充分信息满足最重要的目标。